4. 牛顿运动定律

动力学探索运动与力的关系，其概念由牛顿（）首次提出，即牛顿运动定律——经典力学的基础，解释了常见运动的规律，仅在接近光速或极小尺度时需要修正。

力表示物体间的相互作用。涉及的物体直接接触的力称为接触力，通过接触面作用于物体，如

• 法向力：物体放在或压在平面上，则平面对物体施加垂直于平面的推力。
• 摩擦力：方向与接触面平行，与物体的运动趋势方向相反。
• 张力：通过拉近的绳子或线作用在物体上的拉力。

当物体被真空隔开，还有长程力的作用，如重力、磁铁之间的力。

力的大小的国际单位为牛顿，缩写为 。弹簧的伸长量与力的大小有关，因此，常用弹簧秤测量力的大小。利用多个重量均为 的物体便可标记相应位置，给指针设定标度，由此测量未知力的大小。

实验表明，力是矢量，具备所有矢量的性质。当两个力 和 作用于同一点，其效果与一个力 相当， 为两个力的矢量和 。也称此原理为力的叠加原理。同样，此原理也指导将 分解为 和 方向上的分矢量 和 ：任何力都可以用作用在同一点的分矢量替代。作用在物体上的所有力的矢量和称为合力，用希腊字母 作为求和的简化符号，缩写为

合力 的分量式是一对分量方程：

据此可得合力 的大小和方向：

在力的图示中，若使用分量表示了一个力，则应当在其上画一条波浪线（划掉），明确表示它被替代。

牛顿第一运动定律指出，不受合力作用的物体保持匀速运动，即加速度为零，也可以说，物体拥有惯性。因此，我们称静止或匀速运动的物体是平衡的，平衡物体所受合力为零。

牛顿第一定律适用的参考系称为惯性参考系（惯性系）。地球是近似的惯性系。相对于惯性系做匀速运动的任何参考系都是惯性系。存在加速度的参考系是非惯性系。

实验表明，对于任意给定的物体，如果 是常量，则加速度 是与之方向相同的常量。加速度大小 与物体所受合力大小 成正比。其比值为常数，且与合力大小无关。我们称该比值为物体的惯性质量，或简称为质量，记为 ：

质量是惯性的定量测量：质量越大，物体就越「难以」被加速。质量的国际单位为千克（），牛顿据此定义： 是使得 的物体产生 加速度的合力的大小，即

因此，可以将质量与标准质量对比以测量质量。设相同的恒定合力 作用于质量为 和 的物体，则有

即，对于相同合力，两个物体的质量比与加速度比相反。同时，也可以从一个物体的质量得到另一物体质量。

牛顿第二运动定律指出，有合外力作用的物体加速，加速方向与合外力方向相同。合外力等于物体的质量乘以加速度。

作为矢量方程，其分量形式同样可用：

该方程仅适用于质量 为常量的情况。对于质量变化的情况，则需要使用动量的概念处理。

地球作用在物体上的万有引力称为物体的重量。质量是物体惯性的体现，而重量是地球的拉力作用在物体上的力。由牛顿第二定律可知，对于任意地球表面的物体，要产生自由落体加速度大小 ，必须有力的作用，其大小为

此处的力便是重量。根据上式，相同质量的物体所受重量相同。一般情况下，对于质量为 的物体，其所受重量 可表示为

因此，物体重量大小与它的质量成正比。

是重力加速度 的大小，总是正值。同理，重量大小 也总是正值。

由于地球并非规则球体且存在自转及轨道运动， 的精确值与物体在地面上的位置有关。同理，物体的重量也随位置变化，但质量不变。在特定位置，重量相同的物体也有相同的质量，因此，也能通过测量重量来得到质量。生活中常见的质量数值都通过测量重量得到。

力是相互作用的结果，总是成对出现。牛顿第三运动定律指出，相互作用的两个力大小相等，方向相反，作用在不同的物体上。我们称这两个力为「作用力-反作用力对」。

作用力和反作用力不一定是接触力。牛顿第三定律也适用于不需要物理接触的长程力，如万有引力。作用力-反作用力对中的两个力永远不会作用在同一物体上。

若有拉力作用在物体一端，这个物体就有张力。任一点的张力是作用在这一点上的力的大小。对于绳子来说，若绳子平衡，或是相比下质量很小而可以忽略不计（即视作 ），则根据牛顿运动定律，除了它的两端，其他部位不受力的作用，绳子两端和中间各部分处处张力相等，而作用在绳子上任意点的力矢量和为零。

牛顿运动定律是解决力学问题的基本原理。解题的首要步骤是确定所研究的物体，对平衡的物体使用牛顿第一定律，，以解决平衡问题；对不平衡的物体使用牛顿第二定律，，以解决动力学问题。牛顿第三定律能使作用在不同物体上的力联系起来。一旦确定了物体，便要确定作用其上的所有的力，以得到 。自由体图（free-body diagram，受力分析图）只画出所选择的物体及其所受的所有力的大小和方向，然后建立坐标轴。确保所得的独立方程个数与未知数个数相同。例如，一般情况下，对于二维平面问题，分析一个物体的 、 方向受力可以给出两个方程，若未知数多于两个，则可能需考虑其他物体。

牛顿运动定律的应用

视重和失重

当质量为 的乘客乘坐 方向加速度为 的电梯，其上，秤的读数称为乘客的视重。 为秤施加于乘客的法向力，根据牛顿第三定律，也为乘客向秤施加的力。牛顿第二定律给出

可见，若 为正，即电梯加速向上或减速向下，视重 大于乘客重量 ；反之，若 为负，即电梯加速向下或减速向上，视重 小于乘客重量。若电梯向下加速度 ，即它自由下落，此时 ，乘客失重。

摩擦力

当物体在表面上静止或滑动，我们可以认为表面作用在物体上一个单一的接触力，且该力有平行和垂直于表面的分矢量。垂直分矢量为法向力 ，平行于表面的分矢量为摩擦力 。

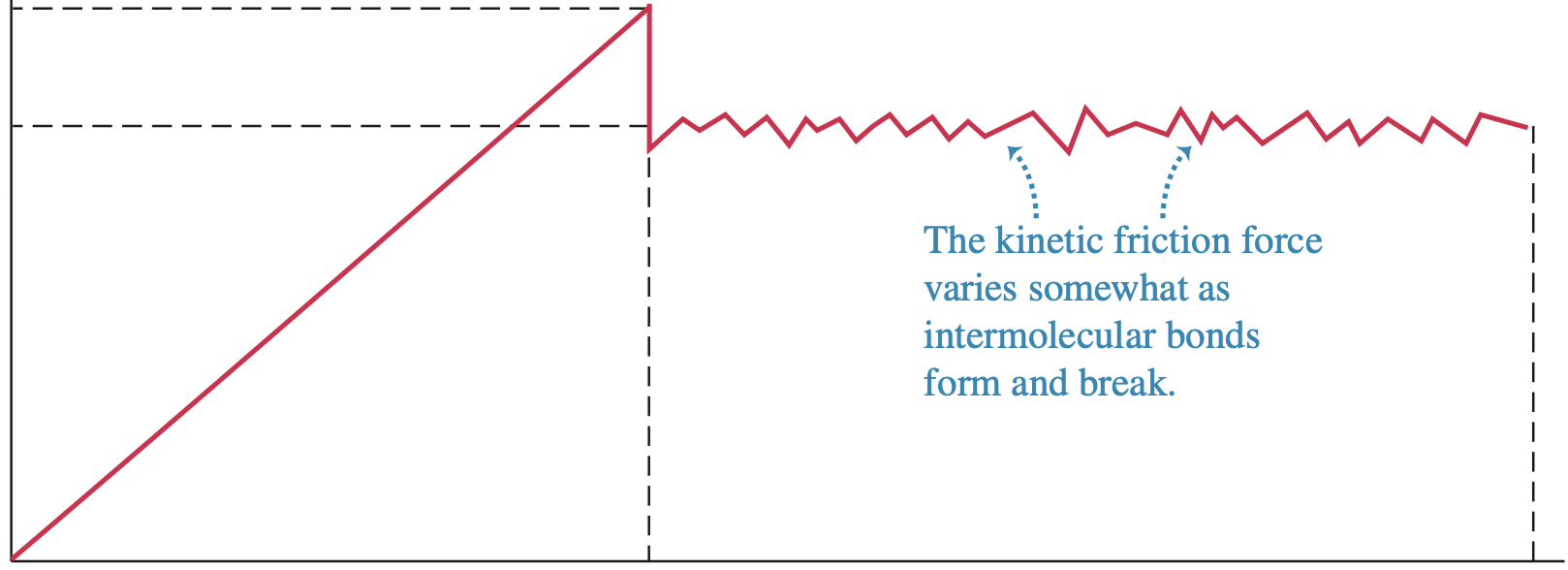
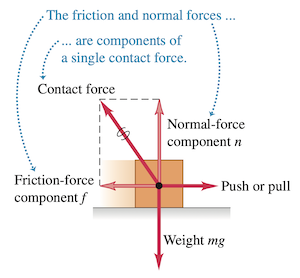微观上，摩擦力和法向力源于两个粗糙表面的接触点的分子间作用力（电力），表面间存在键的形成和断开，且总数会变化，因此，摩擦力并非固定不变。摩擦力的方向总是妨碍相互接触的两个物体的表面的相对运动。若物体在表面上滑动，此时的摩擦力称为动摩擦力（kinetic friction force），记为 。实验上，动摩擦力的大小与法向力的大小成正比，因此，若忽略键的变化和表面相对速度产生的影响，我们据此可得出摩擦这个复杂现象的理想化的近似表达式为

理想化的常数 称为动摩擦因数（coefficient of kinetic friction），取决于表面的光滑程度。表面越光滑， 越小。 没有单位，因为它在数值上为两个力的商 。

没有相对运动时的摩擦力称为静摩擦力（static friction force），记为 。考虑相对运动的临界点，外力足以使得两个表面分子之间的键被打破时，则物体不再平衡，产生相对运动。对于给定的一对表面， 的最大值 大概与法向力成正比：

近似因数 称为静摩擦因数，等号仅在力达到物体开始运动的临界值时成立。若没有外力，。动摩擦因数通常小于静摩擦因数，因此，相对运动开始后，摩擦力通常减小。下图为随外力增大摩擦力的大小。

用轮子滚动比滑动容易得多。滚动摩擦因数 ，又称牵引阻力，为平坦表面上匀速率运动所需水平力除以其法向力。

例：物体沿斜坡静止或滑动，求斜坡角度与动摩擦因数关系。

加速度与质量 无关，是因为作用在物体上的力（重力、法向力、动摩擦力）都与 成比例。显然， 时，加速度为零。 时，加速度为正，，即角度较小时，加速度为负。

流体阻力

流体阻力是流体（气体或液体）作用在穿过它的运动物体上的力，其方向总是相反于物体的速度方向，而大小随物体穿过流体速度增加而增加，与摩擦力非常不同。对于低速物体，其大小大概和物体速率成正比：

为近似常数，与物体的形状和尺寸及流体性质有关。上式适用于如空气中下落的灰尘。对于穿过空气的较大物体，阻力大概与 成正比：

该阻力也称为空气曳力。 与物体的形状和尺寸及空气密度有关。

因此，在流体中下落的物体的加速度不是常量，而要通过牛顿第二定律求得关系式。如，对于低速情况下受流体阻力下落的物体，

初始时刻，，加速度为 。随着速率增大，阻力增加，直到与其重量相等，此时 ，速率和阻力都不再增加。最终的速率 称为终极速率：

现在，实际考虑速度变化过程，要得到速度对时间的表达式，我们将上式中的加速度替换为速度对时间的导数：