4. 应用

绘图

符号表格

微积分知识能帮助确定函数图像的主要特征：从极限到渐近线，从导数到极值。若函数大部分连续，且有少量不连续点，则可以建立符号表格以帮助对函数定性分析。具体做法如下：

1. 以递增顺序将所有零点和不连续点（点之间暂时留空）填入第一行（）。
2. 填充第二行（）对应位置：零点的函数值为 ，不连续点填以星号（）。
3. 空位中填入合适的点，判断并填入对应函数值的符号。 例如，

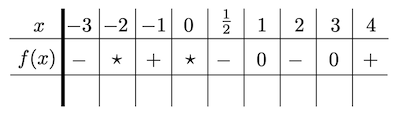
导数符号表格能表示出函数的增减和临界点（极值或水平拐点）。做法与 的符号表格类似，例如，

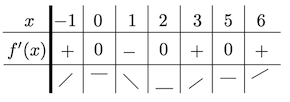
第三行简单画出综合该点及附近的 所能得到的事实。 为正则函数递增， 为负则函数递减；临界点 左正右负则为局部最大值，左负右正则为局部最小值，左右符号相同则为水平拐点。

类似地，可以作出二阶导数复合表格。 为正则函数图像凹向上， 为负则函数图像凸向下，将此信息简单表示在表格第三行。例如，

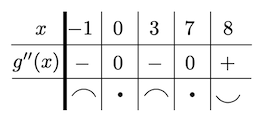
可见， 两侧的凹凸性相同，因此不是拐点。 是拐点。

绘制图像

以下是函数绘图的基本步骤：

1. 检查奇偶性并利用其对称性。
2. 找出并标记 、 轴截距。
3. 检查分母为 的点：若分子同时为 ，则得到可去不连续点，否则为垂直渐近线。
4. 建立符号表格，填入零点、不连续点。
5. 计算函数在无穷处的极限来找出水平渐近线。
6. 求导并分析临界点及其附近的函数行为，标记极值点及其函数值。
7. 求二阶导，检验凹凸性，标记拐点及其函数值。

例 ：不使用导数

较难求导，因此选择 符号表格。 和 有垂直渐近线， 和 为零点。

例

定义于 ， 为临界点， 为零点。分别列出 和 的符号表格即可。同时由于 ，该函数无垂直渐近线。，因此也无水平渐近线。，因此函数图像凹向上，不存在拐点。

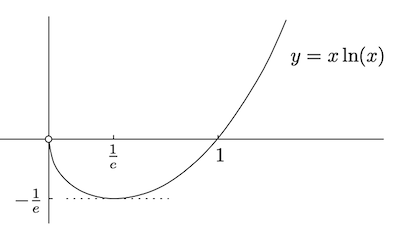
最优化

对于「量」而非「质」来说，根据语境，最优化可能意味着相应地最大化或最小化，通常讨论函数的全局极值。解题时，需要首先将量表示为关于一个变量的函数，例如

两实数和为 ，每个数都不大于 ，乘积的最值是多少？ 解：设两个数为 和 ，需最优化的量 。关注 的定义域，即 的取值范围，根据题意可得 。求导得 ，临界点为 ，因此， 的潜在极值点包括该临界点和两个端点。计算得 ，为全局最大值，，为全局最小值。通过 的符号表格考虑函数变化情况可再次检验上述答案。

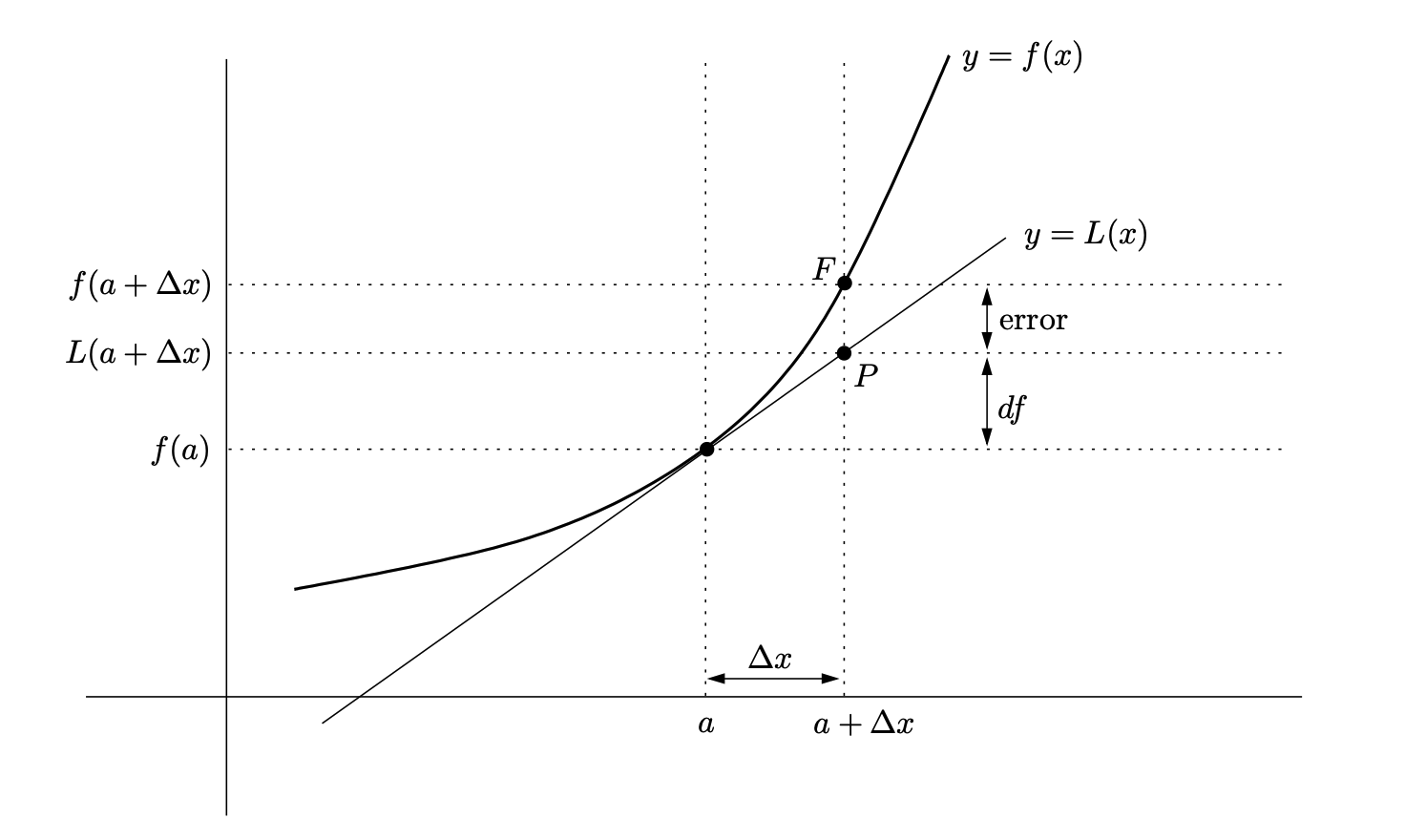
线性化

线性化是使用导数估算特定量的技术。例如，要估算 ，设 ， 附近的已知量为 ，考虑其图像，作出过 的切线，记为 。

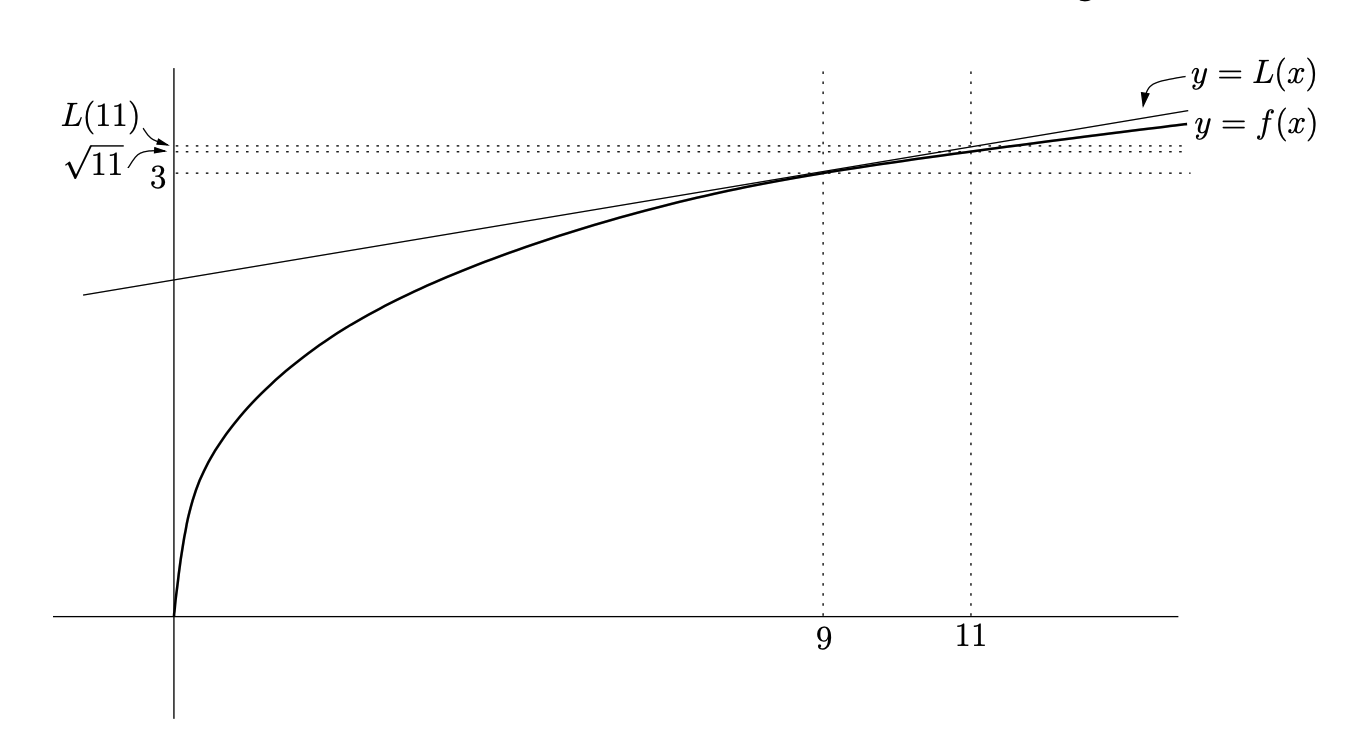线性函数 的斜率即为 ，方程为

由于 ，在 附近，直线 非常接近曲线 。因此， 是对 的很好近似。

一般地，要估算某个量时，首先将其表示为函数 ，然后选取与其接近的、 容易求得的数 ，找到曲线 上点 的切线，记为 ，其斜率为 ，有

线性函数 称为 在 处的线性化。

微分

定义 ，即 ，上式变为

称为 在 处的微分，记为 。