位移、速度和加速度
研究直线运动需要坐标系。我们通常能自行指定坐标轴的方向,例如,选择 轴沿物体运动路径,设起点位置为原点 点。同时,将物体视作质点——选择物体上的一点代表整个物体
位移是由起点指向终点的矢量,位移的 分量即为 值的增量,记为 。
我们用 表示一个量的增量——其终值减去初值。
我们定义质点在时间间隔 内的平均速度 为矢量,其 分量为 的增量除以时间间隔,即平均 方向速度:
瞬时速度表示质点在某一具体时间点或运动路径上某一具体点的速度。为了得到某点的瞬时速度,我们逐步减小 和 (其比值不一定减小),对越来越短的位移和时间间隔计算平均速度 。在微积分中,当 趋近于零, 的极限被称为 对 的导数,写作 。瞬时速度等于位置随时间的瞬时变化率。瞬时速度的 分量——瞬时 方向速度可表示为:
在直线运动这个特殊情况下,我们简称 为位移, 为平均速度, 为瞬时速度,但它们实际上是各个矢量的 分量,因为直线运动中只有 分量。
速度通常指瞬时速度。速率为标量,表示速度的大小。
在位置与时间关系图—— 图中,两点间直线斜率,即三角形垂直边 与水平边 的比值,为质点的平均 方向速度。逐渐减小两点间距离,其值趋近瞬时 方向速度,直至 的极限,直线斜率为该点曲线切线的斜率,即该点的瞬时 方向速度。
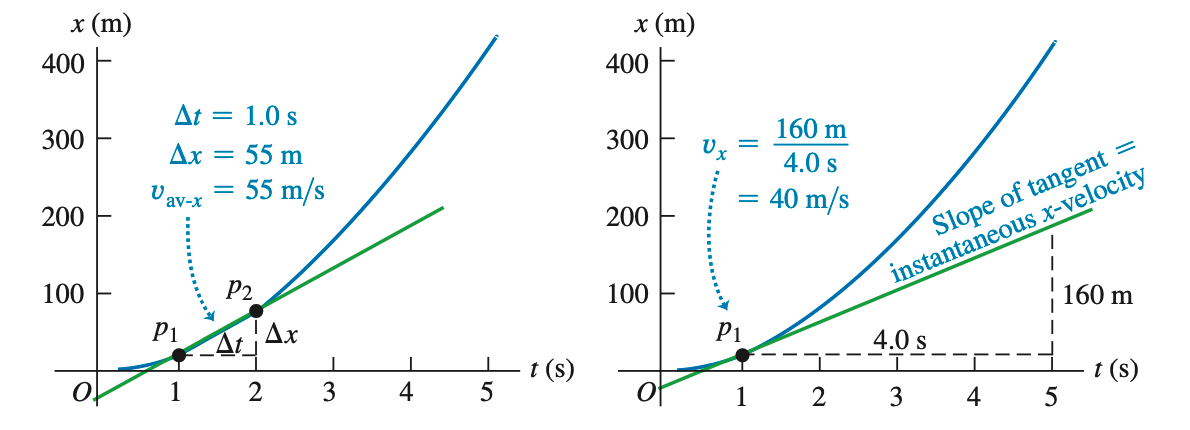
任意点的瞬时 方向速度等于曲线在该点的斜率。因此,观察 图像可知速度的方向。同时使用运动示意图能更好地理解运动。
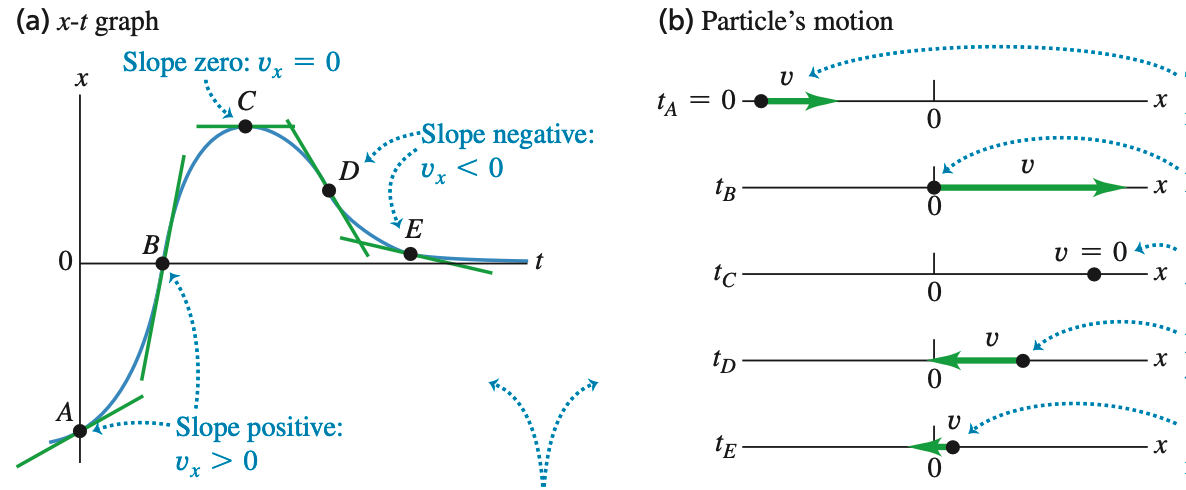
速度描述位置随时间的变化率,而加速度描述速度随时间的变化率,为矢量。质点的平均加速度 分量——平均 方向加速度 等于 方向速度增量 除以时间间隔 :
瞬时加速度是平均加速度在 时的极限——速度对时间的导数。因此,瞬时 方向加速度可通过对 方向速度的时间函数微分表示为:
同样地,对于沿 轴的直线运动,可称 为平均加速度、 为瞬时加速度。
类似地, 图中,任意点的瞬时 方向加速度等于曲线在该点的斜率。此外,可得 是 对 的二阶导数:
任意函数的二阶导数直接联系着该函数曲线的凹凸或曲率。曲线向上弯曲(凹处), 方向加速度为正;曲线向下弯曲(凸处), 方向加速度为负;曲线上没有曲率的点(如拐点), 方向加速度为 。
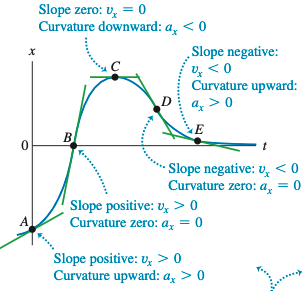
匀加速运动
恒定时物体运动模式较为简单。 图为水平直线, 图为直线。为了导出位置 与 方向速度 对时间的函数,取初始时刻为 ,速度为 ,之后对于 时刻,有:
即,
由于 ,
此外,根据积分中值定理也可得到平均速度的另外两个表达:
因此,
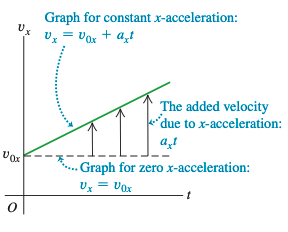
对于匀速运动, 图像为直线。 方向加速度的效果体现于式 。因此,恒定 方向加速度运动之 图总是一条抛物线。
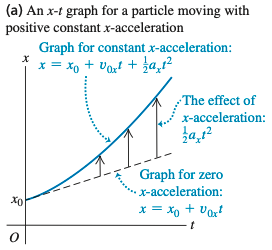
我们还能得到 方向速度与加速度的不含时关系。首先,解出 :
代入位移-时间式:
至此,我们得到了能解决任何 恒定的直线运动问题的公式:
1. 速度-时间公式 (不含 )
表示经过 , 方向速度变化 。不需计算位移。
2. 位移-时间公式 (不含 )
考虑 图像,若 ,则曲线应当为直线。 使得曲线成为抛物线,斜率大小逐渐增加。考虑 图像, 为曲线下方面积。若 ,曲线为水平直线,该部分面积大小为 , 方向加速度使得曲线获得斜率,面积增加了 。
此公式不需计算 时刻速度 。
3. 不含时公式 (不含 )
4. 位移-平均速度公式 (不含 )
匀加速运动解题策略:1. 画图、确定坐标原点和正方向,通常使初时位置()位于原点,则 。2. 指定出现物理量的符号,并将文字转换为物理描述,如「什么时刻达到最高点」意为「 最大时, 为多少」。 3. 使用表格列出已知和未知量,确认可用公式,并画出公式对应图像。4. 对问题的解作定性或定量预测。
自由落体运动
物体受地球重力吸引而下落是最常见的近似加速度恒定的运动,我们称忽略地球自转等影响、视加速度恒定的理想化运动为自由落体运动。自由落体运动的加速度称为重力加速度,记其大小为 ,其地球表面附近的近似值为 ,确切值随位置变化。在月球表面,。
普通直线运动
在更多情况下, 不是常量,匀加速运动的公式不再有效。若已知位置 的时间函数,我们可以通过微分求取 和 。
若已知运动加速度函数 ,由积分知识,任意时间间隔的 方向速度增量 为 曲线下 对应的面积,即 的时间积分:
对 曲线可以进行相同的处理,位移是 方向速度 对时间的积分:
设 ,且 和 分别为 时刻的位置和速度,则上式可改写为:




