导数
切线
描述一条直线需要两个信息:直线上的一点和该直线的斜率。在
当
斜 率 设
斜 率 导函数
函数 称为 导数 ,写作 求导 得到函数 可导 ,有
同样,
上式可阐释为,
若对于特定 不可导 。
上式可进一步改写。
注意,
高阶导数
导数的导数称为二阶导 ,写作
更高阶导数使用相同的方式表示。
可导性和连续性
设
即,
证明,若 可导则连续 」。反之,连续不一定可导。
求导
使用定义
利用导数定义对
即,
对
即,
更一般地,对 为 正 整 数
即,
运算法则
由极限的运算法则,对于函数的常数倍、和差,显然有
为 常 数 对于乘积函数,有
即,
类似地,对于三项乘积,有
对于商函数,有
即,
复合函数链式求导
设
据此推测,若
图像意义
极值
若 极值点 。极值分为全局极值 (绝对极值 )——整个定义域内的极值,和局部极值 (相对极值 )——在某点附近的极值。全局极值也一定是局部极值 。若 临界点 。
极值定理 描述,对定义在开区间
即,开区间内的极值一定出现在临界点。但是,临界点不一定是极值:如,
由于极值点一定是临界点,要求取有限定义域
全局极值显然。考虑
罗尔定理
对于在闭区间 至少 存在一点 至少 有一个临界点。下图为不符合描述的三种情况:
中值定理
对于在闭区间
例如,要证明:反证法 ,假设交点不止一个,任选交点中的两个,记为
中值定理的推论
若
若
二阶导数
拐点 ,因为凹凸性(二阶导数符号)发生了改变。由于函数及其导数连续,
临界点的分类
对于
观察
观察
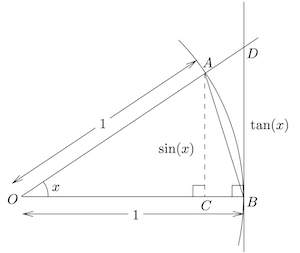
三角函数
三角函数有关极限
扇 形 整理可得到一个重要的不等式:
将上式取倒数并乘以
显然,至此便可根据三明治定理直接写出
考虑
即证明
若接受
因此,便可由
若将
注意到,当
事实上,只要上式分母与分子中正弦或正切的变量匹配,且趋近于
小 数 小 数 和 小 数 小 数 对于变量不匹配的情形,可使用与求解多项式极限问题类似的方法处理。如,
形如
三角函数的导数
利用以上三角函数的极限可求得正弦、余弦函数的导数:
即,
即,
至此便可利用商法则和链式法则求得其他任意三角函数的导数。
即,
即,
即,
即,
隐函数
考虑导数
例如,对于圆的方程
上式表示圆上点
变化率
量 变化率 (rate of change 时间 的导数,即 相关变化率 (related rates how fast one of the quantities changes when the other one changes )。对方程关于
求解相关变化率的一般方法为写出关联所有量的方程、联立求解,求导后代入给定值。
例如,对球体积公式
利用上式便可根据任意时刻的体积变化率和半径求得此时的半径变化率。利用隐函数可将上式表示为另一种形式——体积相对于半径的变化率:
指数函数和对数函数
考虑复利问题,设年利率为
一 年 后 的 原 始 财 富 增 长 倍 数 显然,
设
设
则极限
即,连续 地计算复利时,增长倍数会趋近但不会超过量 增长是指数式的 (虽然事实上「连续」的条件难以达成)。特别地,若年利率
底数为
重新设
事实上,该极限于双侧成立。考虑
总结上述极限,并将
和
对于系数不匹配的情况,可利用指数运算求得极限,如
特别地,
指数函数和对数函数的导数
利用上述极限,则有
即,
特别地,
设
即,
特别地,
取对数求导
处理形如
令
另外一种方法是将指数换底:
然后使用乘积法则和链式法则完成求导。
取对数求导法还能用于简化复杂的涉及幂函数、指数函数的乘积和商的求导,如对下式求导:
对数运算法则可将乘积和商转换为加法,从而简化运算。
指数函数和对数函数的极限
诸如
和 这样的极限是导数伪装的极限,其主要特征为虚拟变量本身在分母上。此处的要点是识别
即,
同样地,上式的
TODO: review
事实证明,在
多 项 式 型 含 指 数 的 多 项 式 型 指 数 函 数 对数函数增长缓慢:
多 项 式 型 对 数 函 数 正 幂 次 多 项 式 型 据此还可推广得到对数函数在
指数增长和衰变
指数增长常见于自然界,如一定条件下的动物种群总数。设
这是一个微分方程 。事实上,
若 , 则 上式描述了 一个量变化的速率取决于其自身大小 。增长常数 。
例如,设
具有放射性的原子经过给定时间存在一定概率发生衰变。考虑一定数量的相同放射性原子,设其在时刻
类似地,方程的解为
称
半 衰 期 为 的 放 射 性 衰 变 双曲函数
双曲函数事实上是指数函数,但又拥有三角函数的特性。双曲余弦函数和双曲正弦函数的定义为
对其平方后作差可得
考虑其导数
即,
与正弦函数、余弦函数表现相似,双曲正弦函数和双曲余弦函数互为导数。
反函数
使用导数易证明反函数存在。考虑
即,
或 即,反函数的导数为原函数在对应反函数值 处的导数的倒数。
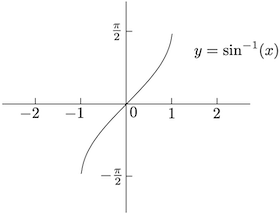
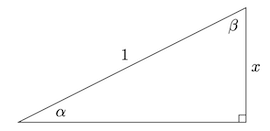
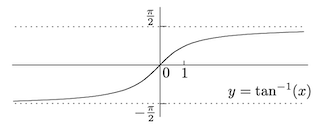
反三角函数
三角函数均有周期性,因而无法通过水平线检验,反三角函数的定义基于定义域的限制。事实上,要使正弦函数
的 定 义 域 为 , 值 域 为 , 是 奇 函 数 。
对其求导:
但事实上,观察
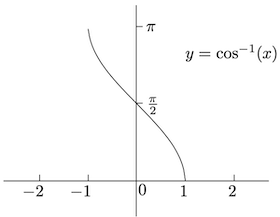
定义时反余弦函数时,
的 定 义 域 为 , 值 域 为 , 无 奇 偶 性 。
类似地,有
由于斜率总为负,因此
可见,反正弦函数和反余弦函数的导数互为相反数,即,
也就是说,
由于
证明反正弦函数和反余弦函数相加为常数
将
的 定 义 域 为 , 值 域 为 , 是 奇 函 数 。
即,
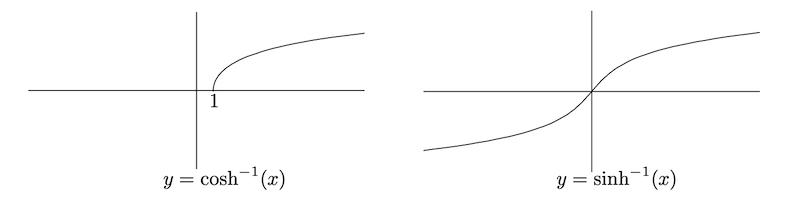
反双曲函数
使用类似的策略得到双曲函数的反函数:
的 定 义 域 为 , 值 域 为 , 无 奇 偶 性 。 的 定 义 域 和 值 域 为 , 是 奇 函 数 。
根据图像,
根据图像,
反双曲函数的对数表示
我们用指数函数表示双曲函数,因而其反函数应当也能用对数函数表示。设
要使上式有意义,
类似地,可以证明
洛必达法则
即使对于连续函数来说,简单的替换有时只能得到 l’Hôpital’s rule )是利用导数求极限的方法。
A )设
若
该情形下,对 线性化 ,
因此,
即,
时 , 例如,
洛必达法则还可以连续使用,如,
事实上,若
可见,分母
B1 )此类极限问题易通过通分及利用共轭式等代数技巧转换为
B2 )类似地,仍然需要将此类极限转化以尝试得到使用洛必达法则的机会。例如,下例中将
此处不转化项
指数(、 、 C )
类似地,对于底数和指数中均含变量的极限,也应考虑对其取自然对数。例如,要求取
至此,我们求得
事实上,由于
又如,求解
因此,
对于极限
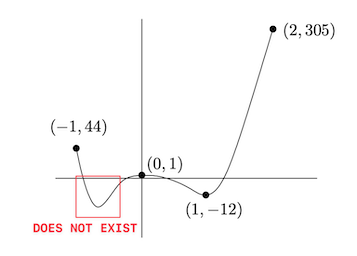
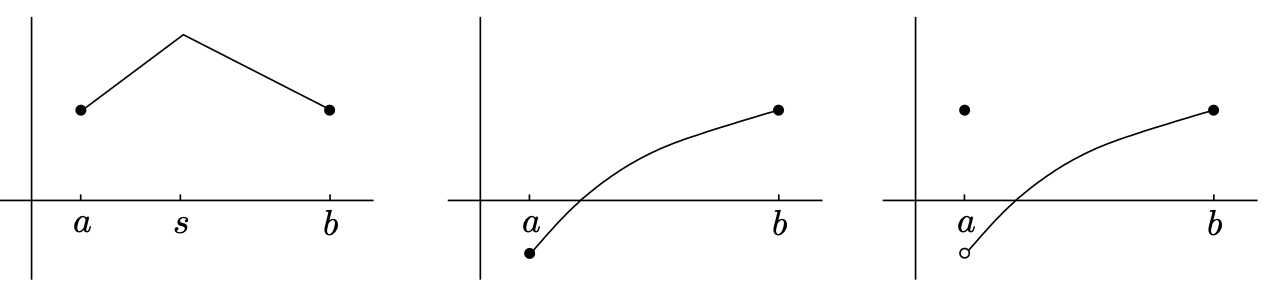
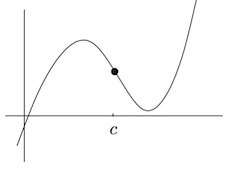 上图所对应函数的二阶导数在
上图所对应函数的二阶导数在