1. 单位、物理量和矢量

物理学是实验科学，我们观察自然现象并试图找到其背后隐藏的规律，这些规律称为理论。建立得完善且广泛应用的规律称为定律或原理。建立物理学理论需要从实验结果中总结出普遍结论，其特点是，我们能用违反理论的现象证伪，但无法证明一个理论永远正确。物理学的新发展常常拓展旧理论的适用范围。

可以用来解决不同物理问题的四个关键步骤是：分析（Identify）、设置（Set up）、计算（Execute）和评价（Evaluate），简称「I SEE」。

• 分析：根据所给条件确定有关物理概念、目标变量，确定问题中明确及隐含的已知量。
• 设置：根据已知信息选择用以求解问题的方程，估计可能的结果，预测系统的物理行为。
• 计算
• 评价：将结果与预测进行比较。假设变量取极值，注意具有特别意义物理量的答案。

理想模型是对物理系统的简化。预测是否有效取决于模型是否有效。

用来定量描述自然现象的任何数都称为物理量。有的物理量只能通过描述如何测量来定义，这种定义称为可操作定义。测量物理量时，我们将其与参考标准比较。例如， 是定义为 长米尺的 倍。这个标准定义为物理量的单位。用数字描述物理量时必须说明所用的单位。科学家和工程师通用的单位系统称为国际单位制（SI）。

我们用方程表示物理量间的关系，方程必须量纲一致，例如：

方程右边的单位 和 互相消掉。计算中，单位像代数符号一样可以相乘或相除。

不确定度或误差表示测量值与真实值间可能的最大差值，取决于所用的测量技术。例如，对于普通的尺子，毫米数量级基本可信，若测量结果是 ，则不能写作更精确的 。有时，不确定度没有明确表示，而是用有效数字位数表示。例如，称书的厚度为 ，其中有三个有效数字，但其实只有前两个数字确定，而第三个数字不确定，不确定度约为 。用有误差的数计算时，得到的结果也有误差。数字相乘或相除时，结果有效数字位数不能大于参与运算的数字当中有效数字位数最少的数字之有效数字位数，如 。相加或相减时，看小数点的位置，如。

矢量

标量可以用一个数字描述，而矢量既有大小又有方向。

矢量加减

设质点依次经过位移 ，结果与其只经过一段位移 达到同一目的地一致。 称为 的合矢量。

矢量相加与次序无关，因此满足交换律。矢量相加需要几何过程，与标量相加不同，我们通常将矢量首尾相连或利用平行四边形法则。根据几何结论：

可以通过矢量相加来做矢量相减：

也可以使 首首相连， 为 末端指向 末端的矢量。

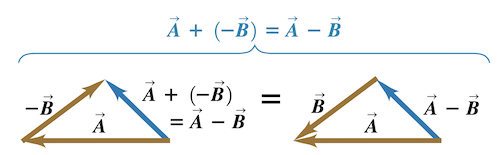
矢量的分量

对于 平面上的矢量 ，它能被平行于 轴和 轴的两个矢量之和表示：

称为 的分矢量。 同时，我们定义：

• 如果 指向 轴正方向： 等于 的大小。
• 如果 指向 轴负方向： 等于 的大小的负值，因为矢量大小不为负。 同理可定义 。 称为 的分量。

我们用相对于参考方向的角度描述矢量的方向。通常设定 ( 轴正方向)为参考方向，

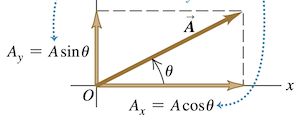
设 与 轴正方向夹角为 ，根据几何结论：

分量计算

使用分量可以简化计算。矢量的大小和方向能与分量相互转换。应用勾股定理， 的大小为：

表示矢量方向：

上式确定矢量方向时可能需要根据 所在象限或 正负进一步确定度数。

设 为 的矢量和：，则 的分量即为被加矢量分量的简单相加：

此过程可拓展至求任意多个矢量之和。

单位矢量

单位矢量没有单位、长度为 ，其唯一目的是描述空间方向。在 坐标系里，定义 为指向 轴正方向、 为指向 轴正方形的单位矢量，则：

和 的矢量和 即可表示为：

同理，三维中引入新的单位矢量 ，则有：

矢量积

普通乘法不适用于矢量。标积得到标量，而矢积得到另一矢量。 标积，又称点积，表示为 ，结果为标量。设二者夹角为 ， 在 方向上的投影（分量）大小为 。（分量可沿任意方向而不限于 轴。） 大小定义为 的大小乘以该分量大小，即：

标积为可正可负的标量。特别地，如果 ，，即相互垂直的矢量标积为零。 例如，恒力 作用于物体使其经过位移 ，力做的功（标积） 为：

因此，现在可将 和 的矢量和大小表示为

标积的分量表示

利用单位矢量的性质可以很容易地用矢量分量表示出其标积。设 和 为三维空间中相互垂直的单位矢量，由于不同单位矢量标积为零，可得：

因此，若各分量已知，便可直接求得夹角：

矢积

矢积，又称叉积，表示为 ，结果为矢量。矢积可用于描述力矩、角动量和磁场。 我们定义矢积 为一个方向垂直于 和 所在平面、大小等于 的矢量。设 ，则：

矢积大小的一个几何解释是 的大小乘以 在垂直于 方向上的分量（）。 为由 转向 之较小角度。，， 如矢量大小一样不为负。因此，共线矢量之矢积为零。特别地，矢量自身之矢积大小为零（矢积为零矢量）。

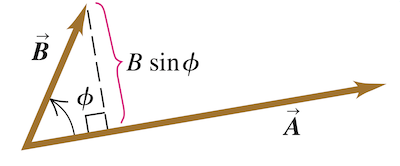
对于矢量 ，标积 和矢积大小 ，若这两个矢量相互平行，则标积之绝对值最大，矢积大小为零；若这两个矢量相互垂直，则标积为零，矢积大小最大。

对于给定平面，总有两个方向与之垂直。要确定 的方向，将两矢量尾部相连，想象 绕垂线沿较小角度旋转至与 平行。使右手四指弯曲并指向旋转方向，拇指便指向 的方向，此规则称为「右手定则」。

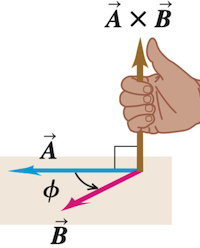
类似地，通过这个规则确定 的方向，所得矢量却与 反向，因为矢积不遵守交换律。 对于任意矢量 和 ：

矢积的分量表示

与用分量表示标积类似，可利用单位向量的性质得出矢积的分量表示。首先，矢量自身之矢积大小为零。 我们使用笛卡尔坐标系（直角坐标系），且总是使用右手坐标系。三维中不同单位矢量间的矢积如图所示。

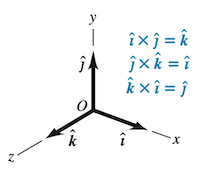
将矢积表达式展开：

由此可得， 的分量为：

对于任意三个矢量 和 ，易通过分量表示证明：