考虑某时刻在点 的质点,其在这一时刻的位置矢量 为从坐标系原点指向 点的矢量,引入单位矢量,可表示为:
质点在时间间隔 内运动,位置矢量变化,则平均速度矢量 可表示为:
引入极限以定义瞬时速度——平均速度在时间间隔趋于零时的极限,即:
与一维运动不同,此时位置 和速度 均为矢量。同时,注意到,这些矢量的 分量即为一维运动中 方向的表达式。对于任意时刻,质点的运动速率为 的大小,运动方向为 的方向。质点上的每一点的瞬时速度矢量与该点轨迹相切。
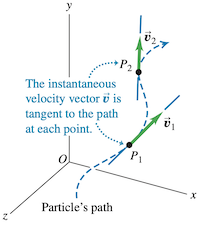
对于任意位移 ,质点各个坐标的变化量 、 和 即是 的各个分量,因此, 的分量 、 和 是各个位置分量对时间的导数,即
上式也可由将位置矢量 表示为对时间 的函数,并对其求导获得:
因此,若已知各个速度分量,便可求得速度矢量:
现在,加速度将描述速度大小和矢量方向的变化。类似地,有
平均加速度是一个方向与矢量 一致的矢量。瞬时加速度 为平均加速度矢量对时间的极限:
同样,加速度矢量的各个分量为对应速度分量的导数、位置分量的二阶导数:
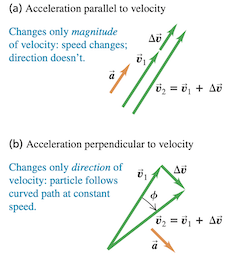
当质点沿曲线轨迹运动,即使其速率保持不变,速度矢量的方向也在时刻变化。因此,这样的运动为变速运动,存在加速度。事实上, 平行于速度的分量 表示运动速率的变化,而垂直于速度的分量 表示运动方向的变化。考虑 时的情况:若加速度 平行于速度 ,则 与 方向相同,即只有速度大小改变;若加速度 垂直于速度 ,则 近似垂直于 ,即其在 方向上没有分量,最终只有速度方向改变。
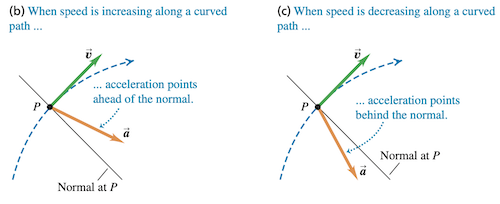
质点沿弯曲路径运动的一般情况下, 指向路径凹侧,加速度使得速率增大或减小取决于其与运动路径法线的角度。
抛体运动
抛体指被给予一定初速度,在重力和空气阻力影响下运动的物体。称其轨迹为弹道。在此我们仅分析忽略空气阻力、地球曲率和自转影响的理想化模型。由于重力加速度方向竖直向下,而不能向侧面加速抛体,抛体运动是二维的,总是限定在由初速度方向决定的 平面内。抛体运动可分解为水平方向的匀速运动和竖直方向的匀加速运动,分别以水平和垂直分量方程表示各矢量关系:
设 时,质点位于 。加速度的水平和垂直分量均为常量,因此可使用匀加速运动公式:
通常将初始位置取作原点,则上式中 。
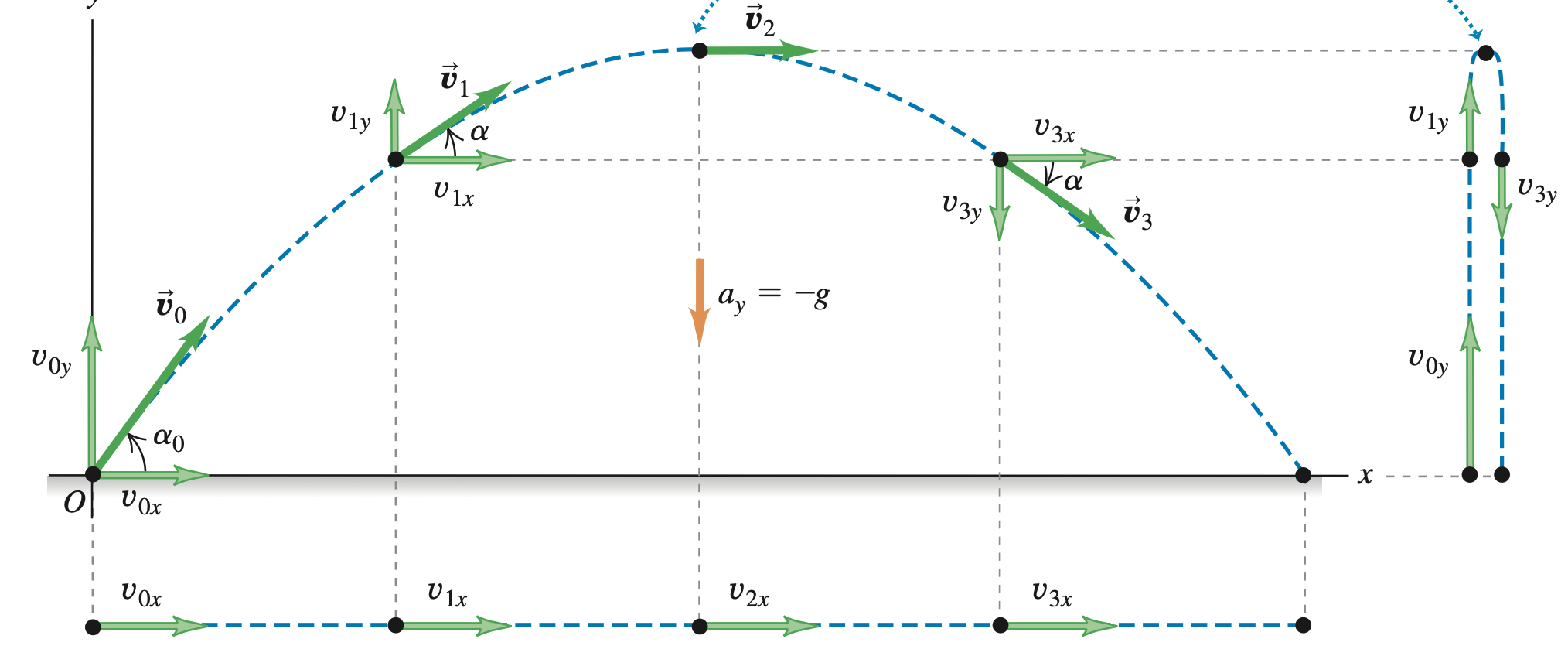
上图显示抛体弹道及其等时间间隔的速度和速度分量。可见, 为常量, 在相等时间内变化量相同。设 与 轴夹角为 ,则 的分量可表示为:
以上述方式表示抛体运动公式(取初始位置为原点):
利用分量和矢量的转换得到任意时刻抛体到原点距离 和速率 :
与 轴夹角 :
从抛体运动位置-时间公式中消除 可得到以 、 表示的抛体弹道方程:
其中,、 为常数。即,在抛体运动的理想化模型中,抛体弹道总是抛物线。
特别地,若初始点和落点在同一水平线上,则质点在最高点时,,。质点在最远处(最大水平距离)时,,。即,落地点时间为达到最高点时间的两倍。对于给定 ,落点 。因此,初始角为 时,,与初始角为 落点相同。
圆周运动
匀速圆周运动中,质点沿圆周做恒定速率运动。此时,加速度没有平行于轨迹的分量,因此,其矢量垂直于轨迹,并指向圆周的圆心。
考虑绕圆心为 ,半径为 的圆周做匀速率运动的质点在时间间隔 内从 运动到 ,距离为 。下图表示出两点上的速度矢量 和 , 垂直于线段 , 垂直于线段 ,因此, 与 夹角 等同于 与 夹角。 内的速度矢量增量 由 末端指向 末端。根据几何学知识,线段和速度矢量构成的两个三角形相似。
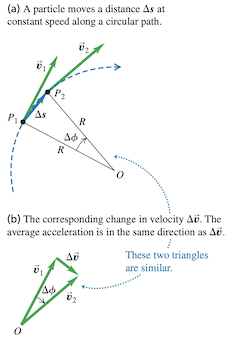
因此,由于相似三角形对应边比值相等,有
据此表示出运动过程中的平均加速度大小:
则瞬时加速度 的大小可表示为
显然, 的极限即为质点在的圆周上任意一点的速率,将其以 表示,则有
该瞬时加速度的方向总是沿着圆的半径指向圆心,因此也称为向心加速度。向心加速度大小保持不变,而方向持续变化从而总是指向圆心。用运动周期 表示质点绕圆转动一周,即距离为圆的周长 所用的时间,则其速率为
代入到匀速圆周运动加速度公式:
对于变速圆周运动,加速度仍有垂直于瞬时速度、指向圆心且与速率成正比的径向分量 ,同时也有平行于瞬时速度的切向分量,等于速率变化率,表示为 ,以强调其与圆相切:
相对速度
某个观察者观察到的速度称为相对于该观察者的速度,简称相对速度。每个观察者都能构成参考系——坐标系加时间轴。
设参考系 、,在一维运动中, 点相对于 系的位置表示为 ,相对于 系的位置表示为 , 的原点相对于 的原点的位置表示为 ,则有
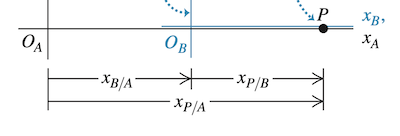
点相对于 系的 方向速度可表示为
上式描述了各个速度沿直线的相对关系。
若 和 是任意的参考系或点,那么
若题目涉及相对速度,应画出和表示每一个参考系。此外,地球表面(其上任意静止点)这个参考系几乎总是要用到。用标示符号确定目标变量,如 表示 相对于 的速度。
相对速度的概念可通过矢量加法拓展至更高维度。使用位置矢量替代 坐标:
同理可得速度矢量:
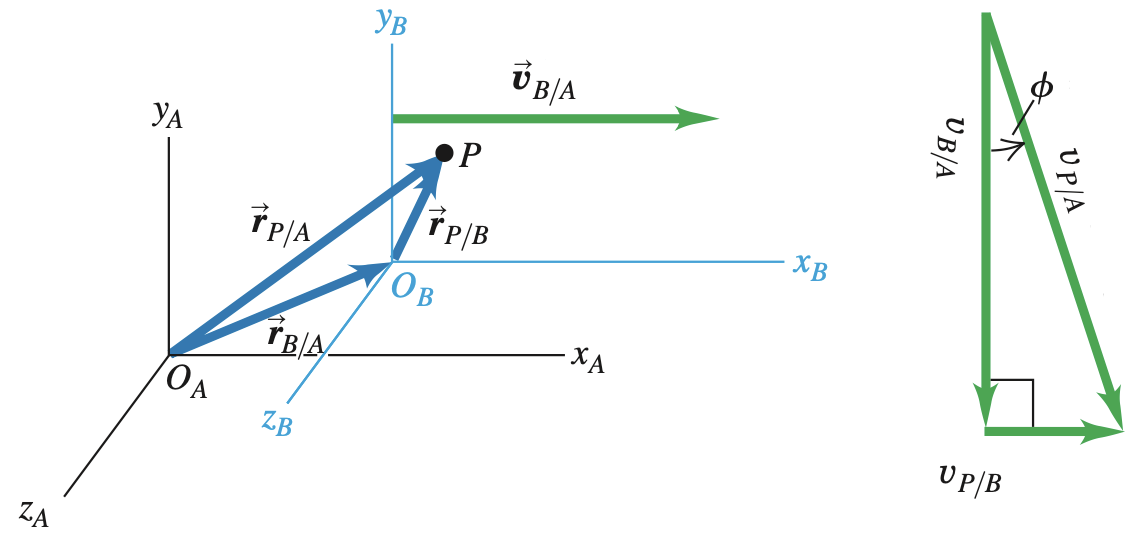
上图中 与 正交,因此还能通过勾股定理求得






