基本思想
设函数 ,当 沿数轴从左侧或右侧趋近于 时, 趋近于 ,即:当 时,,记为:
上式的正式定义表示对于任选的 ,可以选取 ,使得对于所有满足 的 ,有 。即能找到一个 使得 到 的距离小于 时, 到 的距离小于 。
此处的 表示 在 附近的双侧极限,即左极限和右极限。上式等价于:
如果左极限和右极限不相等,则极限不存在。例如:
在 处有一条垂直渐近线。垂直渐近线表示 或 至少有一个为 或 。另外, 则表示 在 处有一条右侧水平渐近线。
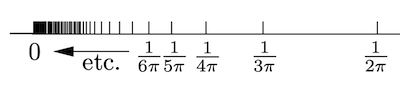
在 时为极限不存在的另一种情况。 为 的 轴截距,当接近 时,其与 轴交点越来越密集,且无限地在 至 之间振荡,所以 不存在。由于 , 在 处有水平渐近线。
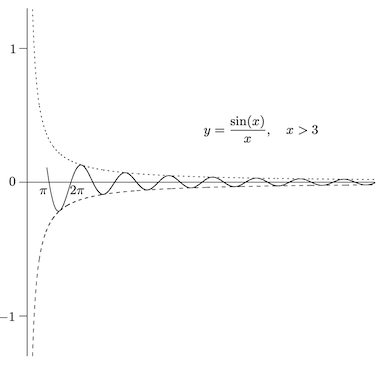
一个与其渐近线相交的例子为函数 。。 在 到 振荡,即 在 到 振荡。曲线 和 形成正弦波的包络。
三明治定理
若对于所有在 附近的 ,都有 ,且 ,则 。即若当 时,夹挤函数 的两个函数 和 收敛于同一个极限 ,则 也收敛于极限 。证明仅需任选 ,有
例如 ,所乘的 使得 陷于包络之间。
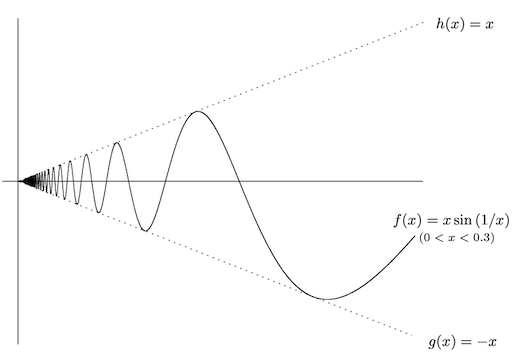
由于 ,设 ,则有 。又由 ,应用三明治定理可得 。
从定义证明极限
从定义证明极限通常很复杂。以证明 为例,选取 ,则 被限制在 。需要理解,所选 越小, 可选的范围就越小。考虑 的情形时,应当很容易能够找到满足定义的 。假设所选的 ,不妨设 , 被限制在 ,我们有:
又因为 :
利用上述不等式,可表示出:
至此便证明了对于任选的 ,可以相应地选取 ,使得只要 满足 ,则 ,满足 成立的定义。
由原极限产生新极限
我们可以在合理的范围内对极限做四则运算和使用三明治定理以得到更多极限。
和差
设 ,,选取 ,并将 限制为充分接近 (选取较小的 ),以保证 ,。我们希望证明 时, 接近 。据三角不等式 可得:
即,和的极限等于极限的和。同理可证:
乘积
类似地,对 和 作差:
选取 ,有 ,,将 限制为充分接近 ,例如,我们假设所选 使得 ,即 ,也就是 。将这些不等式代入上述不等式:
据此重做一次以上步骤,使得 , 同理,便可得到:
即证明:
特别地:
商
商的极限等于极限的商,与乘积的极限证明方法类似。
求解多项式极限问题
多项式之比称为有理函数。对于有理函数 的 附近的极限 ,若用 替换 后 ,则替换后所得的值就是极限值。例如,
若替换后 ,则 处有一条垂直渐近线。
若替换后的值为 ——不定式,则极限不确定。借助因式分解及其他代数技巧或可求解,例如:
对于多项式的极限,当 趋近于无穷时,首项决定一切。首先,对于任意的 , 为常数,有
因此,
在处理有关多项式的无穷极限时,常用的方法是:若关于 的多项式 多于一项,将其代以
例如,
可见,要点是「萃取出各首项」,而其他各项不产生影响。以上是严谨的数学论证过程。
对于最终得到的比值,若:
- 的次数等于 的次数,则极限有限且非零;
- 的次数大于 的次数,则极限无穷;
- 的次数小于 的次数,则极限为 。
另外,上述求解极限的结论和方法也适用于包含根式或绝对值的多项式型函数,在使用时应特别注意符号。
连续性
函数 的一点 处连续意味着一连串点 越来越接近于点 ,即该点的连续要求 时,。即,
函数在区间上连续表示其在区间内的每一点都连续。对于形如 的区间,双侧极限在端点处不存在,因此只要求单侧连续,即 ,。如果函数在定义域内所有点都连续,则称该函数是连续的,即,
函数 保持极限是连续的核心思想。由于对极限做四则运算仍保持极限,连续函数也是如此:对连续函数做四则运算,则得到另一个连续函数。常数函数显然连续,对于 ,,因此 也连续。之后便可利用四则运算证明任意一个多项式都是连续的,因此,对于多项式 ,其极限可表示为
也就是说,求解多项式极限时,可以直接代入。另外,指数函数、对数函数和三角函数都是连续的。
连续函数的复合
设 和 连续。任选 上一点 ,由于 连续, 在 上连续,即 。由于已知该极限成立,因此,设 ,对于任选的 ,一定可以选取 ,使得对于满足 的 都有 。同时, 在 上连续,即 ,因此,可以选取 ,使得当 时,有 。综上所述,对于满足 的 ,有 ,即,
证明 连续。
介值定理
若函数 在 上连续, 且 ,则 轴截距存在于 上的某处,即, 上存在一点 ,使得 。介值定理的一个变体是将 替换为任意数 ,即,若 且 ,则 上存在一点 ,使得 。
例如,对于任意的奇数次多项式 ,当 趋近于无穷时, 收敛于首项 ,也与其符号相同:
设 为一个很大的负数, 为一个很大的正数,则一定有:
因此,
根据介质定理,在 和 之间有一个数 ,使得 ,证明 有一个根。
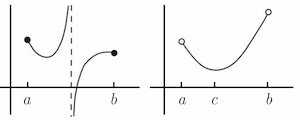
连续函数的最值
若函数 在闭区间 上连续,则它在 上至少有一个最大值,位于 处,使得 。最小值同理。不连续可能导致的问题包括:
- 渐近线产生不连续点,可能导致没有最大值或最小值
- 开区间端点未定义,下图没有最大值