函数
函数是将对象(输入)转化为另一对象(输出)的规则。输入来自定义域,输出来自上域。函数必须给每一个有效输入指定唯一输出。值域是所有可能输出所组成的集合。
反函数
给定函数
要检验是否满足定义反函数的条件,可以使用水平线检验:如果每一条水平线与函数图像相交至多一次,则这个函数有反函数。对于检验失败的函数,在限制其定义域后便可能满足定义反函数的条件。
例如,令
复合
我们可将复杂函数的计算分解为前后相继的独立的计算并各描述成一个函数。以
线性函数
线性函数形如
或可理解为
该公式称为直线方程的点斜式。若已知直线上两点
多项式
称由数个不同系数的基本项
多项式图像左右两端的走势由首项,即最高次项之系数
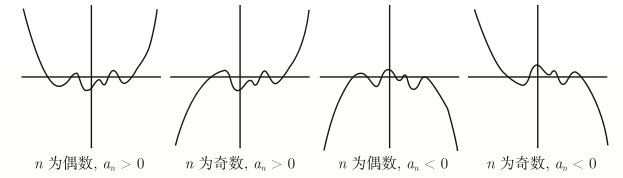
综合以上形式总结可得,若
指数函数和对数函数
设
换底法则
对于任意对数函数,有
可见,所有不同底数的对数函数互为常数倍:
因此,
对于任意指数函数,有
三角学
三角恒等式
根据毕达哥拉斯恒等式,有
上式两边分别同除以
三角函数名中的音节开头「co」为「互余」(complementary)的简称。我们称互余的两个角之和为
例如,